東京大学 大学院新領域創成科学研究科 複雑理工学専攻
岡田真人
© 2024 Masato Okada
１．データ駆動科学
図1に示すように、2011年2月にScience誌において、データ科学特集が企画された[1]。図１のその特集号の中の論文で、天文学における高次元データ解析手法(画像処理)が、全く対象とスケールが異なる生命科学でも有効に働くという内容が紹介されており、このようにスケールや対象が異なる場合でも、同じアルゴリズムが有効に働くので、データ科学を創成されそうであると論じている。
しかし、そこには、なぜ、スケールや対象が異なる場合でも、同じアルゴリズムが有効に働く理由を探るという態度は全くみられなかった。そこで我々は、その理由を問い、背景にある普遍性からデータ解析自体を学問的対象とする枠組みであるデータ駆動科学の創成を目指した。
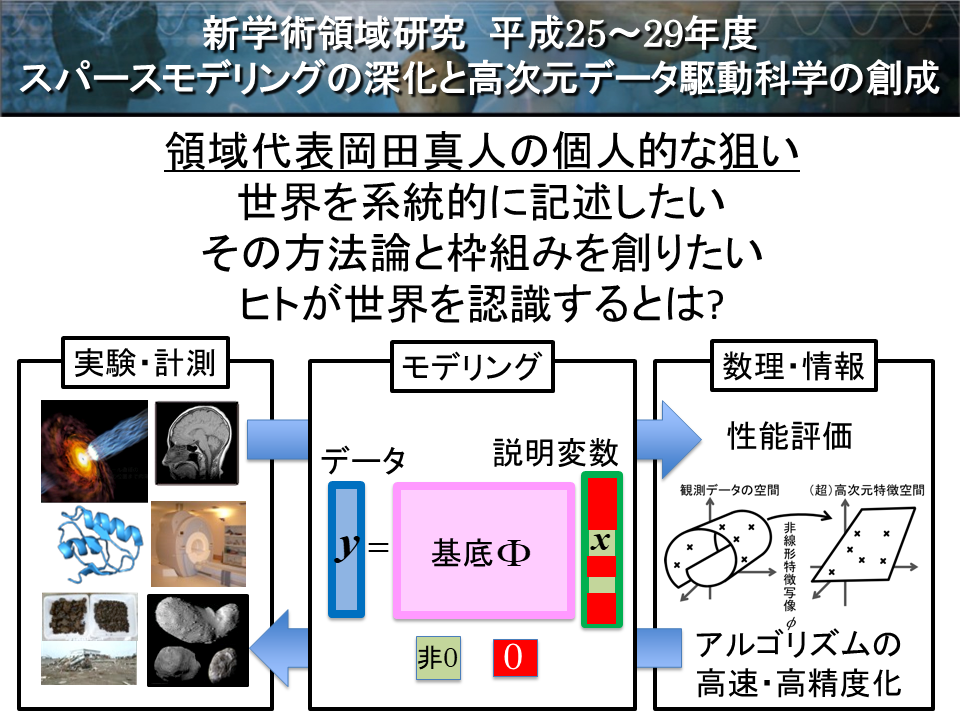それを基盤に、我々は、文部科学省科学研究補助金「新学術領域研究」平成25 年度〜29年度スパースモデリングの深化と高次元データ駆動科学の創成Initiative for High-Dimensional Data-Driven Science through Deepening Sparse Modeling (略称 新学術SpM)を開始した。
http://sparse-modeling.jp/
２．計算論的神経科学とDavid Marrの三つのレベル
後述するように新学術SpMの2013年10月末最初の打ち合わせの際に、データ駆動科学を推進し創成することがいかに難しいかを実感する体験を持った。私は、新学術SpMの推進し創成をスムーズに行うことを、領域代表の属人的才能で行うのではデータ駆動科学の創生はあり得ないと考え、データ駆動科学のパラダイムを明確化する必要があると考えた。その際に、強く影響されたのがイギリスの神経科学者David Marr（1945年1月19日 – 1980年11月17日）
https://ja.wikipedia.org/wiki/%E3%83%87%E3%83%93%E3%83%83%E3%83%89%E3%83%BB%E3%83%9E%E3%83%BC
が彼の著書Vision[2]で提案した、David Marrの三つのレベルである。
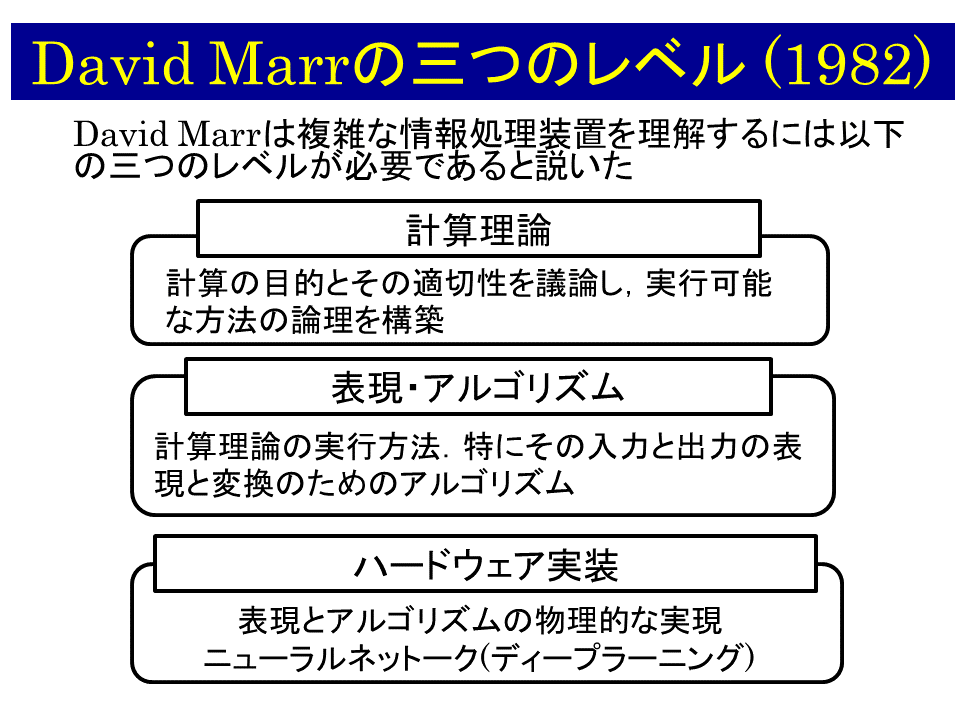このパラダイムは同時の脳神経科学の状況からすると革新的であった。通常、脳や神経系を研究するには、脳神経系を構成する神経細胞や、その神経細胞のネットワークであるニューラルネットワーク、つまり脳のハードウェアを研究するのが当然であると考えられていた。
事実、David MarrもCambridge大での博士学位論文では、現在Marrの三部作と呼ばれる、総ページ数300ページの、小脳の理論、大脳古皮質の理論、大脳新皮質の理論で、脳のハードウェアの研究を行っている。これら三つの論文は、その後の脳のハードウェアの研究の方向性を決定づけるものであった。小脳の理論では、小脳はパーセプトロンであると提唱し、大脳古皮質の理論では、大脳古皮質は連組記憶モデルであると提唱している。さらに、大脳新皮質の理論では、大脳新皮質は分布を表現するとしている。これらすべて、ことの本質をついており、現在も、このパラダイムで脳のハードウェアの研究は推進されている。
このような実績により、David MarrはMITのAIラボの教授に招聘される。驚くべきことにここで、David Marrは、脳はハードウェアレベルの研究だけでは理解できないと宣言する。そして、脳は情報処理機械であるという側面を重視した、図3の David Marrの三つのレベルを提唱する。
ハードウェアの研究は具体的でよくわかるが、計算理論と言われても抽象的でよくわからない。そこで、MarrとPoggioによる両眼立体視を例に取り、David Marrの三つのレベルを説明する [3]。両眼立体視とは、左右の網膜像の対応点を探し、その対応関係をつかって、網膜像では顕に表現されていない、奥行方向の情報を推定する問題である。
この問題の計算理論の計算の目的は、両眼の対応問題を解くことである。しかし、この問題は不良設定性を持ち、そのままでは解を一意に決めることは出来ず、適切ではない。そこで、網膜上で近い点同士の奥行きは近いという拘束条件を導入して、問題を適切化する。計算理論の下のレベルの表現とアルゴリズムのレベルでは、計算理論で導入された拘束条件を数理的に表現する。右と左網膜に対して、それぞれ1次元の場を用意し、その1次元の場で、奥行きを表現する。そして、1次元の場の間に、近い点同士の相互作用を導入し、計算理論で導入された拘束条件を表現する。そして、それら二つの1次元場に評価関数をいかのような評価関数を導入する。その評価関数の最初の項は、各1次元場に一つだけ値を取り、そのほかの部分は0になるような項である。二つの目の項は、二つの1次元場の相互作用を表し、片方の1次元場で1が立つところの近くに、もう片方が1を取りやすいような項である。そして、その評価関数を最少化するアルゴリズムで、両眼立体視の問題を表現し解く。このようにMarrとPoggioは両眼立体視の、計算理論と表現・アルゴリズムを論じた。この両眼立体視の話は、脳の機能の研究において、計算理論と表現・アルゴリズムを用いる必要があることを示す良い例である。
David Marrは、脳を複雑な情報処理機械である立場をとり、複雑な情報処理機械一般を理解する戦略として、計算理論、表現・アルゴリズム、ハードウェア実装の三つのレベルを分けて考えるべきだというパラダイムを宣言している(Marr Vision 1982)．ここでいう複雑な情報処理とは、両眼立体視のように、与えられた条件だけでは解が一意に決まらず、他の条件を導入しなければならない情報処理課題のことを言う。
３．データ駆動科学の三つのレベル
3-1. スペクトル分解の三つのレベル
後述するように新学術SpMの2013年10月31日(木)のハロウィンに東大駒場キャンパスで開かれた最初の領域会議の際に、図4のベイズ的スペクトル分解[4]の紹介を私が行った時のことである。
スペクトル分解の計算理論の計算の目的は、多峰スペクトルに埋め込まれた複数の離散的な電子構造を、スペクトルデータから抽出することである。スペクトル分解は、非常に多くの物理学/化学/生命科学/地球惑星科学などの応用分野が存在する。物理学/化学/では、X線光電子分光スペクトル(XPS)、物理学/化学/生命科学では核磁気共鳴スペクトル(NMR)、地球惑星科学では月の表面の分光スペクトルなどである。
ここで複雑な情報処理であるスペクトル分解を、図6に示すように、David Marrの三つのレベルで整理してみようこの計算の目的を遂行するには、多峰性スペクトルをガウス関数などの単峰関数の線形和で表現し、その線形展開する際のガウス関数の数Kを決める必要がある。しかし、ガウス関数の数Kを適切に決める方法がすぐには思い当たらない。ガウス関数の数Kを適切に決めないと、電子状態を多峰スペクトルか推定するという計算の目的が達成できなくなる。ガウス関数の数Kを大きくすれば、多峰スペクトルの近似精度はどんどんあがっていく。しかし、そうすると、きっと多峰スペクトルの観測データに過適用してしまう。そこで、ベイズ推論の知見を導入し、ベイズ的モデル選択で、ガウス関数の数Kを決めると言う戦略を用いる。電子状態を推定すると言う計算の目的を達成するために、ここで計算理論の下のレベルの表現とアルゴリズムのレベルの議論になり、多峰スペクトルをK個のガウス関数の線形和で表現し、多峰スペクトルを再構成するベイズ的モデル選択のアルゴリズムをもちいて、電子状態を推定することにした。この方針は成功に終わり、その結果を学術論文にまとめることができた[4]。
このようにして構築したベイズ的スペクトル分解の紹介を終えようとした時、機械学習研究者が、ガウス関数のような基底関数を無限個で、多峰スペクトルを近似する方法があるとコメントしました。ガウス過程回帰のことです。これに、すぐに反応したのが実験研究者で、ガウス関数の数Kが無限ならもっとすごいことができるのではないかと興奮し出しました。
ここまでの私の説明を読んだ方は、この興奮が全く的外れなことはよくわかると思います。基底関数無限個で多峰スペクトルを高精度に再構成できても、それはスペクトル分解の計算の目的を達成できてないものです。
ここで、私は異分野融合の真の困難さの理由がよくわかりました。通常、異分野融合では使っている言葉の定義が違うので、議論にならないと言う話がありますが、それは誤りです。いくら言葉の定義を一致させても、異分野融合の困難さは解消しません。ことの本質は、データ解析が、David Marrが指摘したように階層的な構造をしており、現在どのレベルの議論をしており、そのレベルの議論が、他のレベルの議論と矛盾がないかをチェックしながら研究を進めるということをこれまで経験したことがないことが、異分野融合の困難さの原因です。同一分野内では、どのレベルの議論をするかがあらかじめ決まっており、他のレベルのことを意識して議論する必要がないので、このようなトレーニングが秀才であると信じられている通常の研究者にはできていません。
3-2. David Marrの三つのレベルが示唆すること
私は、新学術SpMの推進し創成をスムーズに行うことを、領域代表の属人的才能で行うのではデータ駆動科学の創生はあり得ないと考え、データ駆動科学のパラダイムを明確化する必要があると考えました。そこで思いついたのが、2.で紹介した両眼立体視の問題とベイズ的スペクトル分解の相同性です。この相同性から、スペクトル分解のような自然科学のデータ解析も、脳が解いているような複雑な情報処理に属する問題であることがわかります。スペクトル分解でも、データだけからはガウス関数の数Kを決めることができずベイズ的モデル選択を援用せざるを得ません。また両方とも、表現はベイズ推論をもちいます。そこから、David Marrの三つのレベルから示唆されるデータ駆動科学の三つのレベルが導出できる可能性が見えてきました。
3-3. データ駆動科学の三つのレベル[5]
そこでDavid Marrの三つのレベルを参考にすると、以下のように図7のデータ駆動科学の三つのレベルに到達する。まずデータ駆動科学では、つかうハードウェアはノイマン型のコンピュータなので、ハードウェア実装を議論する必要はない。つぎに、その代わりに、計算理論と表現・アルゴリズムの間に、モデリングを導入しました。データ駆動科学では、ヒトが計算理論の目的や方略を数理モデルに変換する必要があります。
ここで重要な点は、データ駆動科学のこれまでの研究から、表現とアルゴリズムでは、ベイズ推論またはスパースモデリング(SpM)を用いることで十分であることが経験的にわかっています。データが生成されるメカニズムが数理モデルとしてある程度わかっており、解を一意に定める必要がある時に拘束条件を事前確率の形で自然にモデリングできるのがベイズ推論です。一方、データの生成機序が不明な場合、データを再構成するための特徴量をたくさん用意して、それを刈り込むスパースモデリング(SpM)が用いられます。これらベイズ推論とスパースモデリングだけでデータ解析ができることも、脳と自然科学データ解析の相同性です。
3-4. 連立方程式とデータ駆動科学
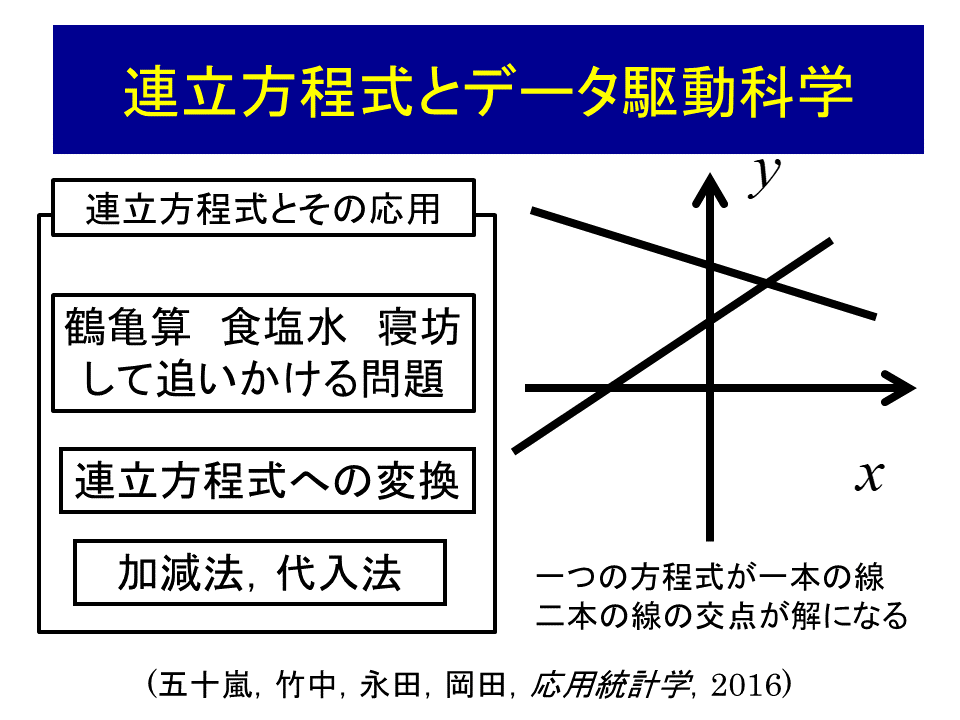このデータ駆動科学の三つのレベルの構造は、図8の中学二年生で学ぶ連立方程式の応用問題を考えると容易にわかります。連立方程式のモデリングと表現とアルゴリズムのレベルは連立方程式と加減法、代入法です。データ解析の目的にそうとする部分は、つるかめ算、食塩水の問題、おねえちゃんと弟が遊園地に行く約束していて、弟が寝坊をして、おねえちゃんを追いかける時の速度を求める問題などです。このような森羅万象多様な対象が、連立方程式で全てモデル化でき、連立方程式でかければ、加減法と代入法で問題の多様性を考えずに解けるという構造を、なんと我々は義務教育の中学二年生の数学で学んでいるのです。ここにも、多様な計算問題がモデリングと表現・アルゴリズムで、連立方程式と、加減法/代入法と類型化され、パターン化されていることを学んでいます。図3の新学術SpMも、図9に示すように、連立方程式とその応用と全く同じ構造を持ちます。我々の新学術SpMは、これまで存在したすべての大型研究プロジェクト中で、一番取り扱う範囲が広いです。そのことにより、新学術SpMは高く評価されています。しかし、その背景は、これまで述べたように義務教育の中二の連立方程式とその応用と全く同じ構造だということに注意する必要があります。ビジネスとしてデータ解析についても、義務教育で学んだ大切な連立方程式の構造との相同性があることをすっかり忘れてしまっています。
このような結果、2016年のDeepMindのAlphaGoの登場の際に、AIが職業を奪うとか、気楽に深層学習でビジネスになると思って、こけた企業が続出しています。AlphaGoは確かに深層学習を使って驚くべき能力を発揮していますが、その背景にはきちっとデータ駆動科学の三つのレベルで解釈できる理由があります。AlphaGoでは、囲碁のデータを強化学習で学習し、その学習に関数近似能力の高い深層学習を使っているわけです。AlphaGoの計算理論は強化学習で、表現とアルゴリズムが深層学習です。そういう背景をまったく考えずに、深層学習というハードウェアに乗る、高度な関数近似器があれば、どんな問題でも解けると踊っても利益が出るはずはありません。つまり、データ駆動科学の三つのレベルにもとづく戦略こそが、基礎研究の推進をスムーズにするとともに、高収益を上げることができる企業体制を作る鍵になります。その高収益化の鍵は、本来はデータ解析を依頼する顧客が計算理論のレベルをデータ解析企業が請け負うことです。さらに、重要な点は、顧客が計算理論である、データ解析の目的、その目的を達成するための方略をしらないケースの方が、圧倒的に多いです。そこで、顧客をインタビューして、顧客のための計算理論を構築できる技術者が必要で、その人が、会社の高収益を担っているのです。
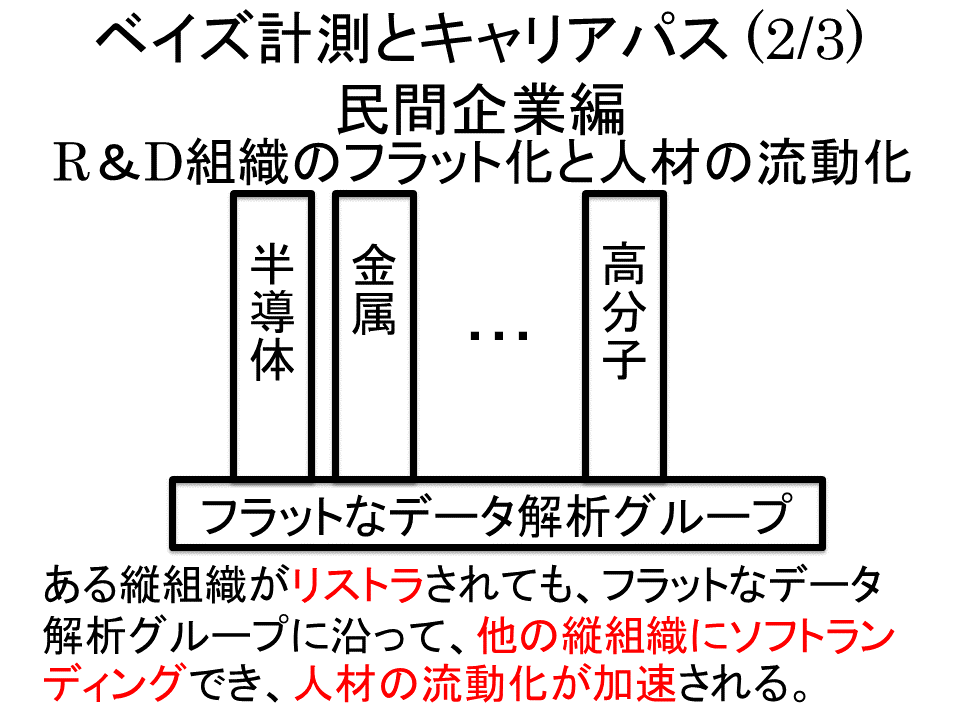これを基礎研究に当てはめると、実験家自らが行っている実験の目的や実験データから知りたい情報を抽出できる訪略を知らないことも多いです。多くの場合、深く考えて実験しているわけでなく、先生や先輩がやっていることを無批判に反復しているだけなので、なにか状況が変わった場合の対処の仕方がわからないわけです。そこに必要なのは、実験家でもなく理論家でもないデータ駆動科学研究者です。データ駆動科学研究者は実験家より、実験の目的や実験データから知りたい情報を抽出できる訪略をよく知っており、理論家よりも、その系の理論的な機序をよく知っている必要があります。大学や企業では、図8のような横串の立場をとる、サッカーのミッドフィルダーのような役割を果たします。
[1] SCIENCE VOLUME 331|ISSUE 6018|11 FEB 2011
[2] David Marr Vision: A Computational Investigation into the Human Representation and Processing of Visual Information (Mit Press
[3] Marr and Poggio, Cooperative Computation of Stereo Disparity, Science, New Series, Vol. 194, No. 4262. (Oct. 15, 1976), pp. 283-287
[4] Nagata, Sugita and Okada, Bayesian spectral deconvolution with the exchange Monte Carlo method, Neural Networks 2012
[5] Igarashi, Nagata, Kuwatani, Omori, Nakanishi-Ohno and M. Okada, “Three Levels of Data-Driven Science”, Journal of Physics: Conference Series, 699, 012001, 2016.
